Grijper/hand
Uiteindelijk werd er beslist om een "hand" te maken met 3 vingers, deze vooral geïnspireerd door de concepten van Sten en Teun. Dit werd bepaald met behulp van een morfologisch overzicht:
| Criteria | Concept Tom | Concept Camiel | Concept Adrian | Concept Sten | Concept Teun | Concept Godfried | Concept Ferry | Maximaal |
|---|---|---|---|---|---|---|---|---|
| Grip | 5 | 6 | 7 | 9 | 8 | 7 | 7 | 10 |
| Budget | 8 | 9 | 8 | 8 | 7 | 7 | 8 | 10 |
| Langzaam omhoog | 7 | 8 | 7 | 7 | 7 | 7 | 7 | 10 |
| Horizontale verplaatsing | 7 | 6 | 7 | 8 | 8 | 6 | 6 | 10 |
| 15cm tillen | 6 | 7 | 6 | 8 | 8 | 7 | 7 | 10 |
| Stabiliteit | 6 | 6 | 7 | 7 | 7 | 7 | 7 | 10 |
| Sterk | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 10 |
| Mogelijkheid tot grijpen | 5 | 7 | 7 | 8 | 8 | 7 | 7 | 10 |
| Elegantie | 5 | 5 | 5 | 8 | 8 | 7 | 5 | 10 |
| Totaal | 57 | 62 | 62 | 71 | 69 | 63 | 62 | 90 |
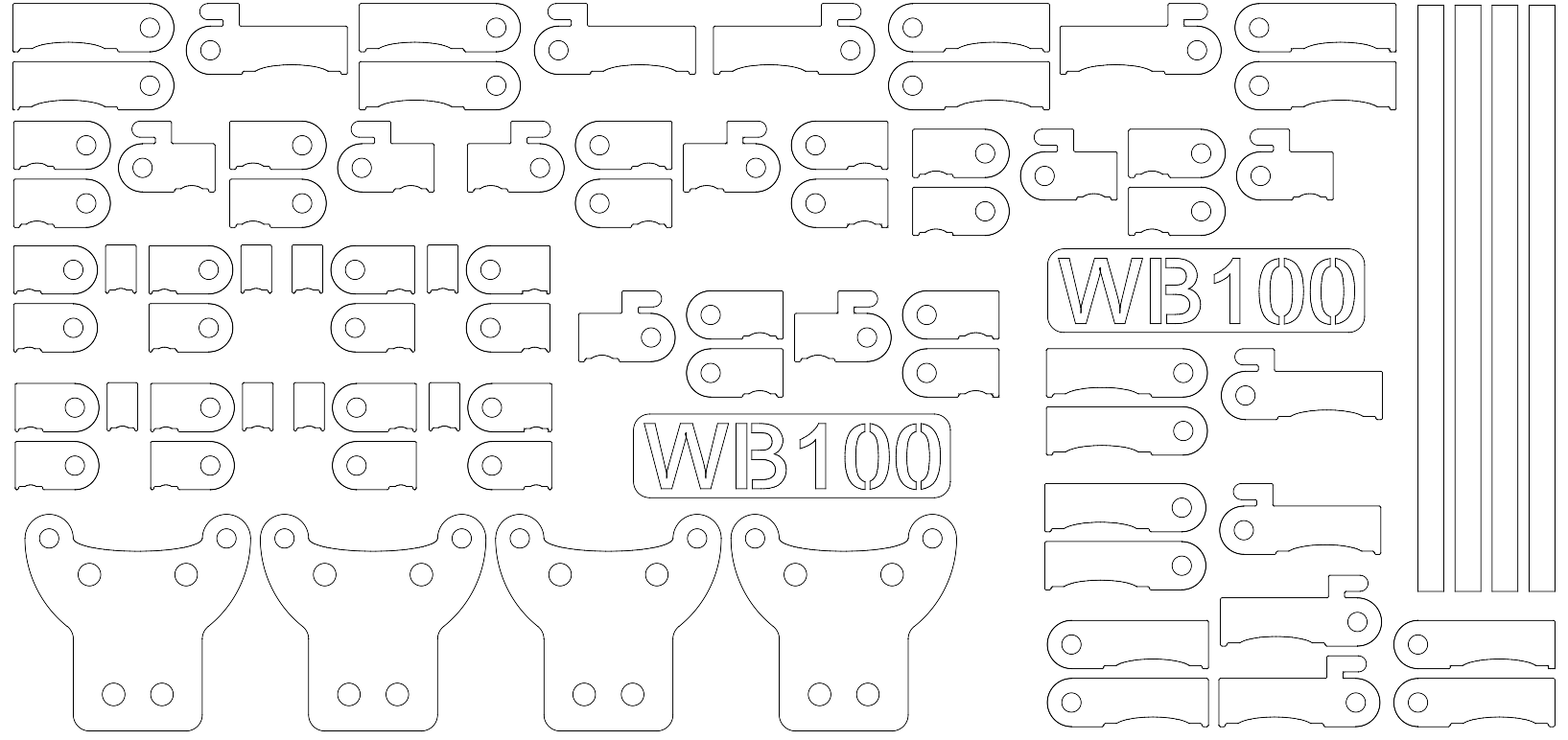 Vervolgens moesten de vingers terug naar hun oorspronkelijke stand. Dit werd opgelost door uitsteeksels aan de eerste 2 kootjes te plaatsen waartussen een elastiek (wat een veer werking heeft) werd gezet. Deze uitsteeksels dienen ook als barrière zodat de kootjes niet
helemaal terug klappen.
Om voor meer wrijving te zorgen met het voorwerp werd er per kootje een inhammetje geplaatst waar een materiaal/stof kan worden geplaatst met een hoge wrijvingscoëfficïënt. Er werd namelijk voor rubber gekozen. Naast een hoge wrijvingscoëfficïënt kan rubber tegelijkertijd een beetje indeuken. Dit laatste is ideaal omdat de vingers zich voor verschillende vormen kunnen aanpassen.
Vervolgens moesten de vingers terug naar hun oorspronkelijke stand. Dit werd opgelost door uitsteeksels aan de eerste 2 kootjes te plaatsen waartussen een elastiek (wat een veer werking heeft) werd gezet. Deze uitsteeksels dienen ook als barrière zodat de kootjes niet
helemaal terug klappen.
Om voor meer wrijving te zorgen met het voorwerp werd er per kootje een inhammetje geplaatst waar een materiaal/stof kan worden geplaatst met een hoge wrijvingscoëfficïënt. Er werd namelijk voor rubber gekozen. Naast een hoge wrijvingscoëfficïënt kan rubber tegelijkertijd een beetje indeuken. Dit laatste is ideaal omdat de vingers zich voor verschillende vormen kunnen aanpassen.
Verplaatsing
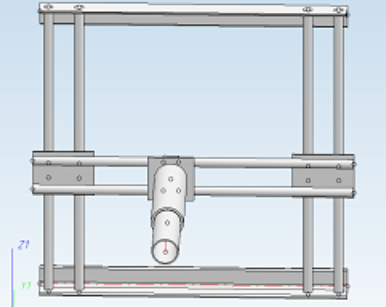 Verder was er ook een bewegingsmechanisme nodig. Om dit vrij simpel en net te houden werd een gekozen voor een rail-systeem. Deze kan zich gemakkelijk in de x- en y-as verplaatsen met behulp van actuatoren.
Een andere reden dat er voor de rails werd gekozen hebben is dat met de rails het bekertje recht omhoog bewogen wordt en dit is niet het geval bij het vierstangenmechanisme. Hierbij is het ook mogelijk dat er een kantelbeweging van de grijper plaatsvindt, dit moet namelijk heel beperkt worden gehouden.
Eis: "op een circa 150 mm hoger en naast gelegen plateau kan neerzetten."
Hoewel er in x-as geen probleem heerst, het moet zich maar een paar cm verplaatsen, is er wel een probleem voor de y-as. De actuatoren kunnen namelijk maar 10 cm uitschuiven terwijl er 15 cm nodig is. Dit wordt later opgelost met behulp van katrollen op bepaalde plekken.
Verder was er ook een bewegingsmechanisme nodig. Om dit vrij simpel en net te houden werd een gekozen voor een rail-systeem. Deze kan zich gemakkelijk in de x- en y-as verplaatsen met behulp van actuatoren.
Een andere reden dat er voor de rails werd gekozen hebben is dat met de rails het bekertje recht omhoog bewogen wordt en dit is niet het geval bij het vierstangenmechanisme. Hierbij is het ook mogelijk dat er een kantelbeweging van de grijper plaatsvindt, dit moet namelijk heel beperkt worden gehouden.
Eis: "op een circa 150 mm hoger en naast gelegen plateau kan neerzetten."
Hoewel er in x-as geen probleem heerst, het moet zich maar een paar cm verplaatsen, is er wel een probleem voor de y-as. De actuatoren kunnen namelijk maar 10 cm uitschuiven terwijl er 15 cm nodig is. Dit wordt later opgelost met behulp van katrollen op bepaalde plekken.
Matlab
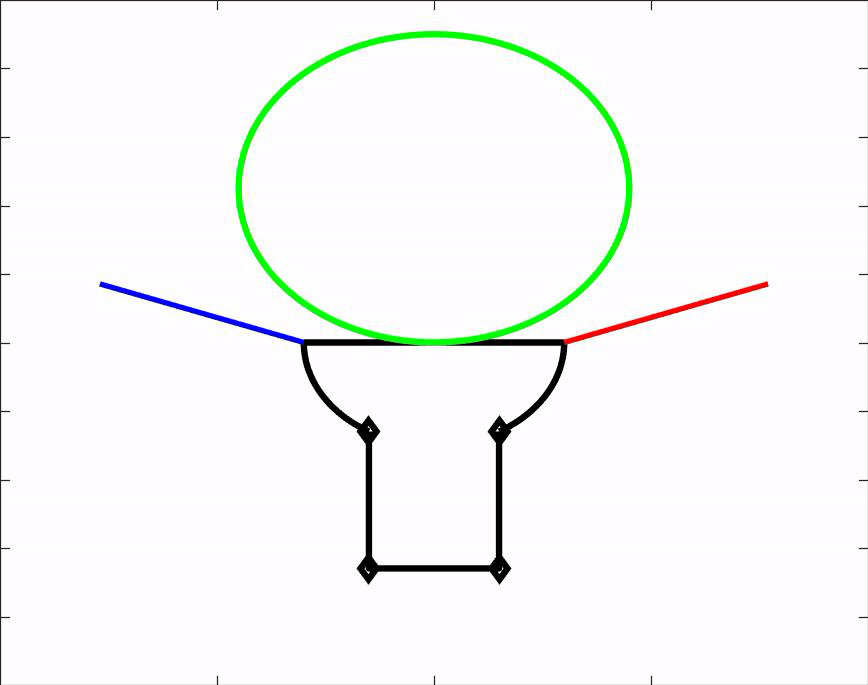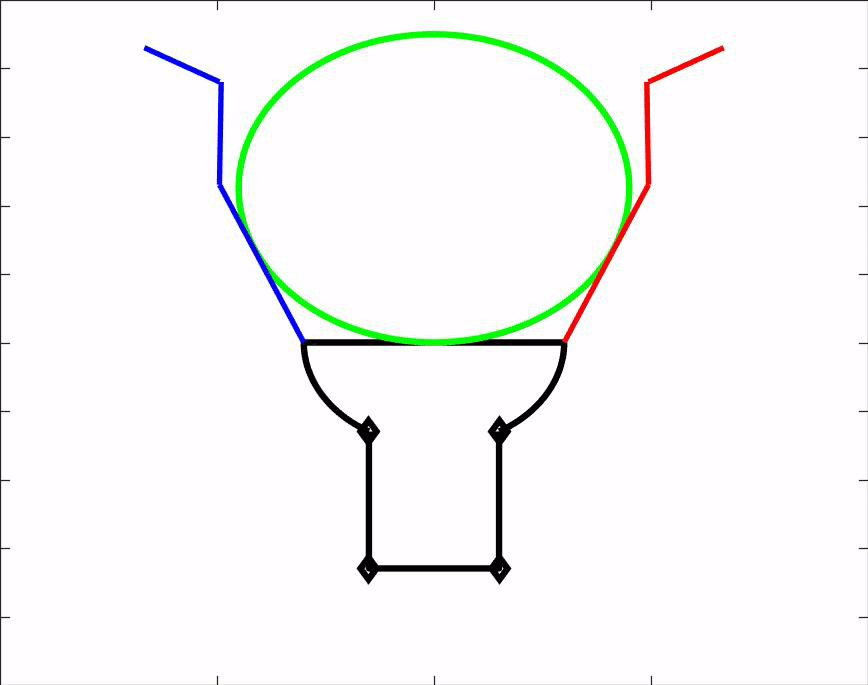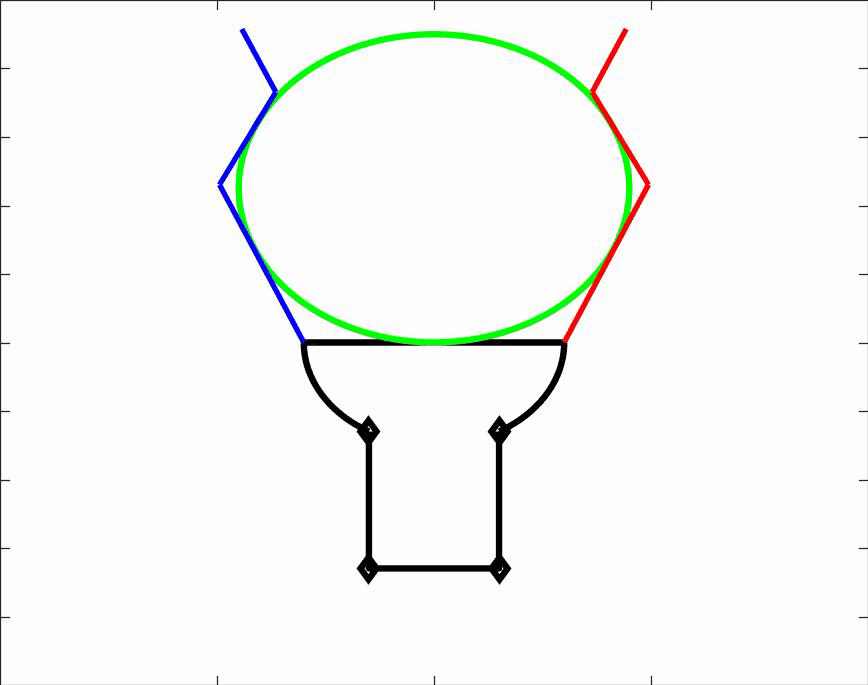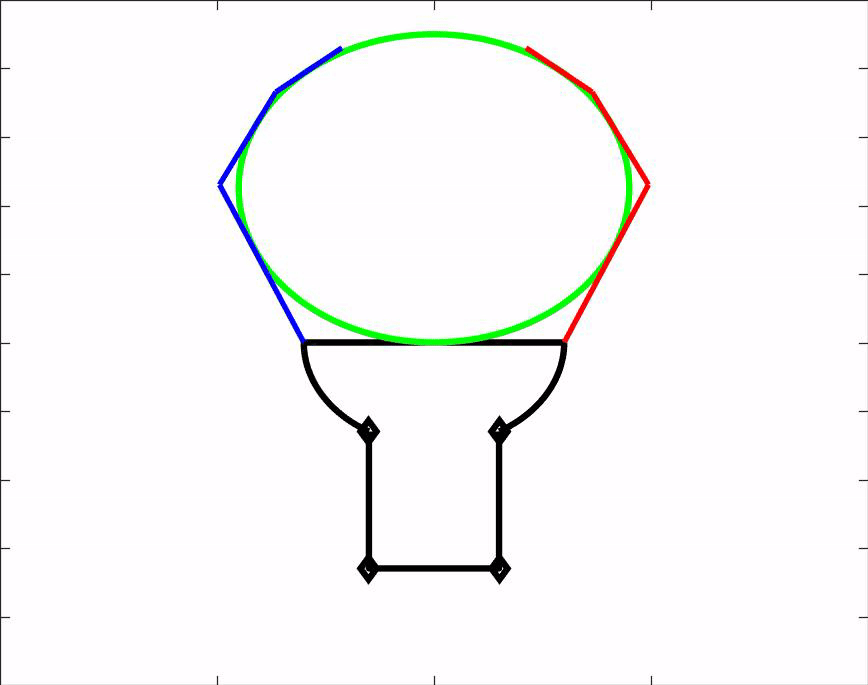
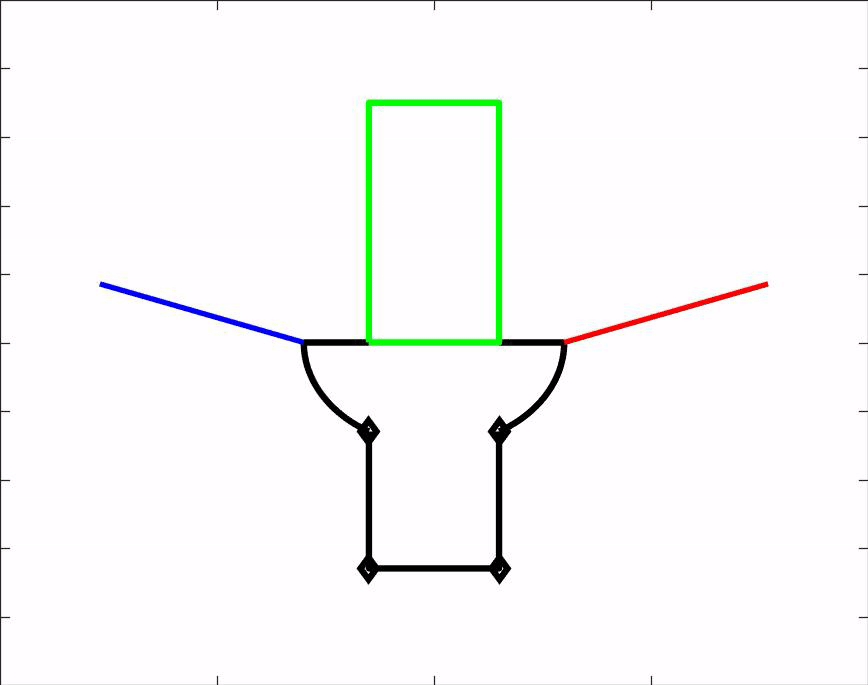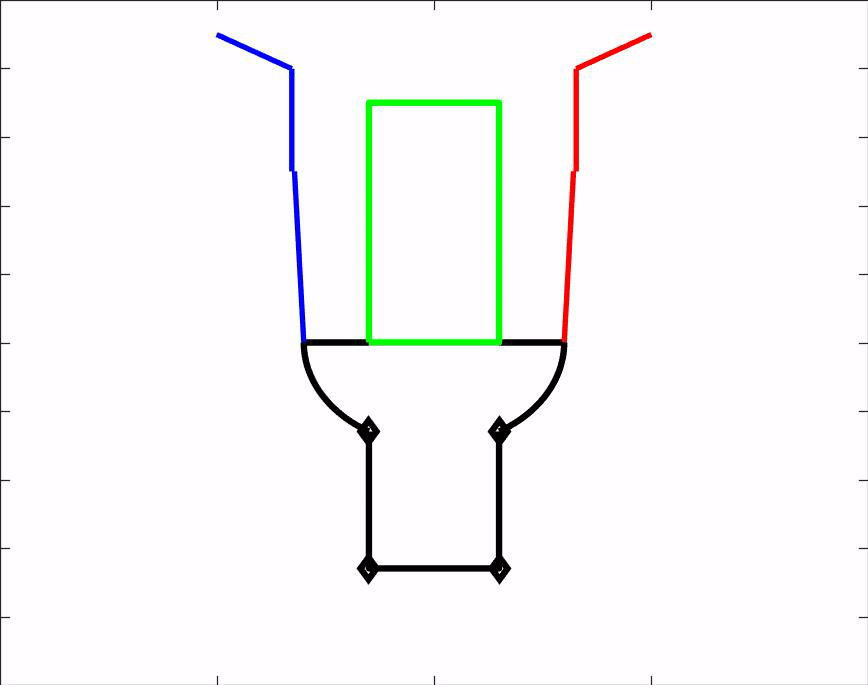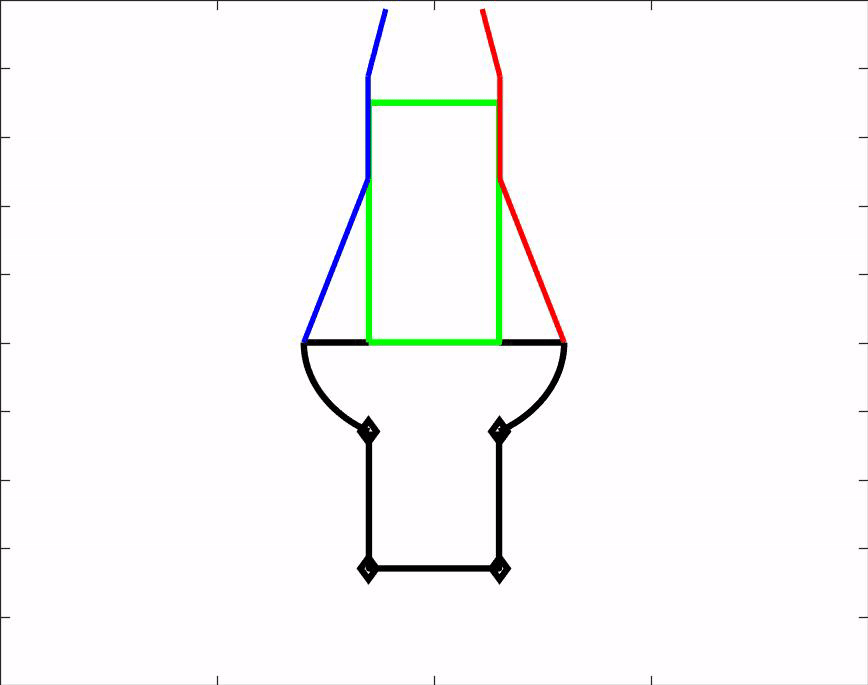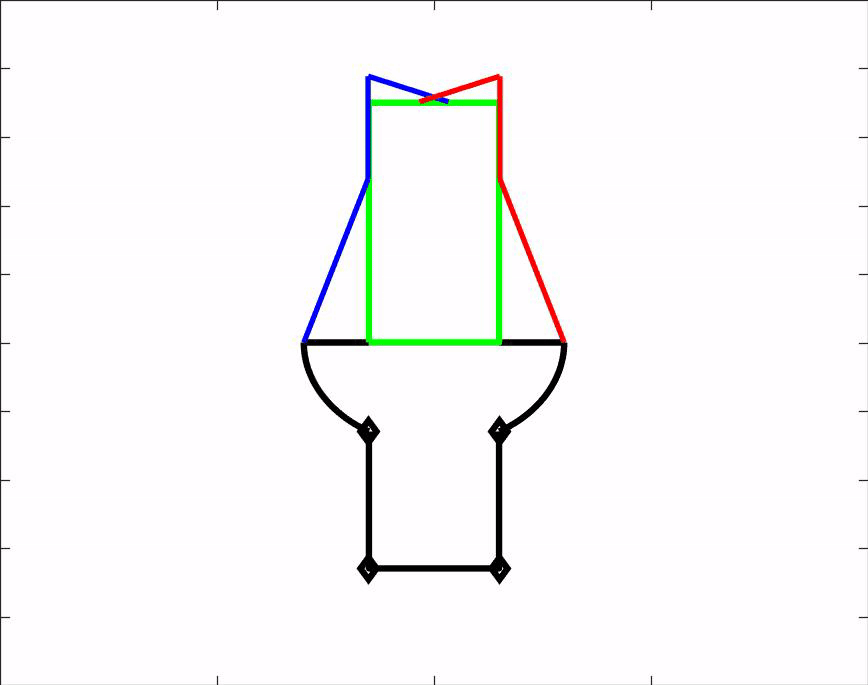
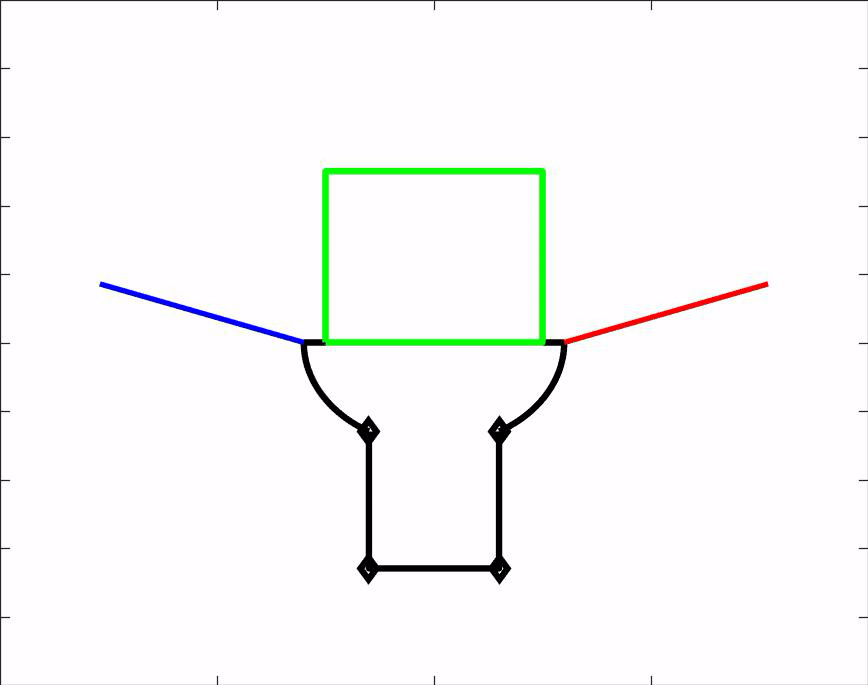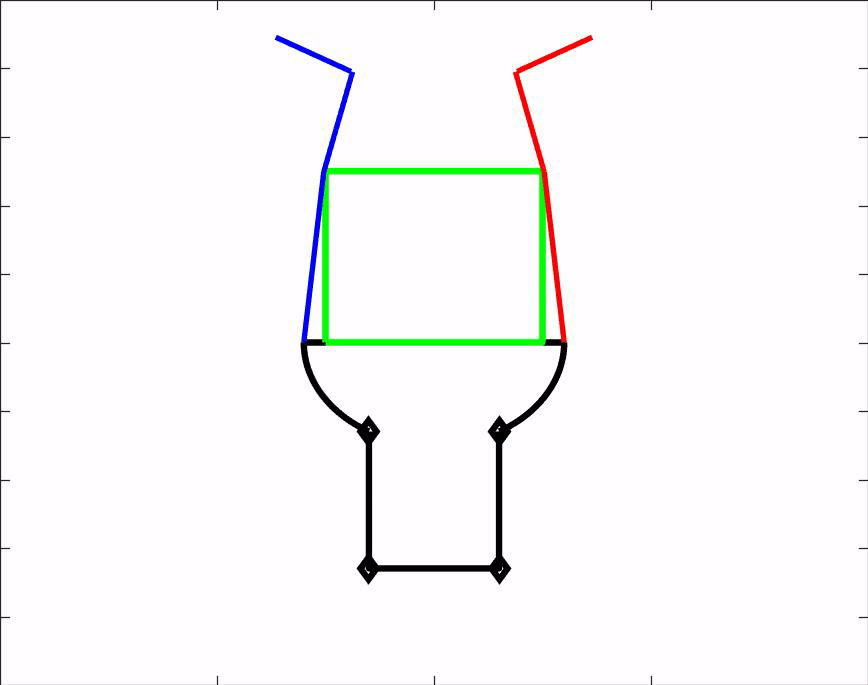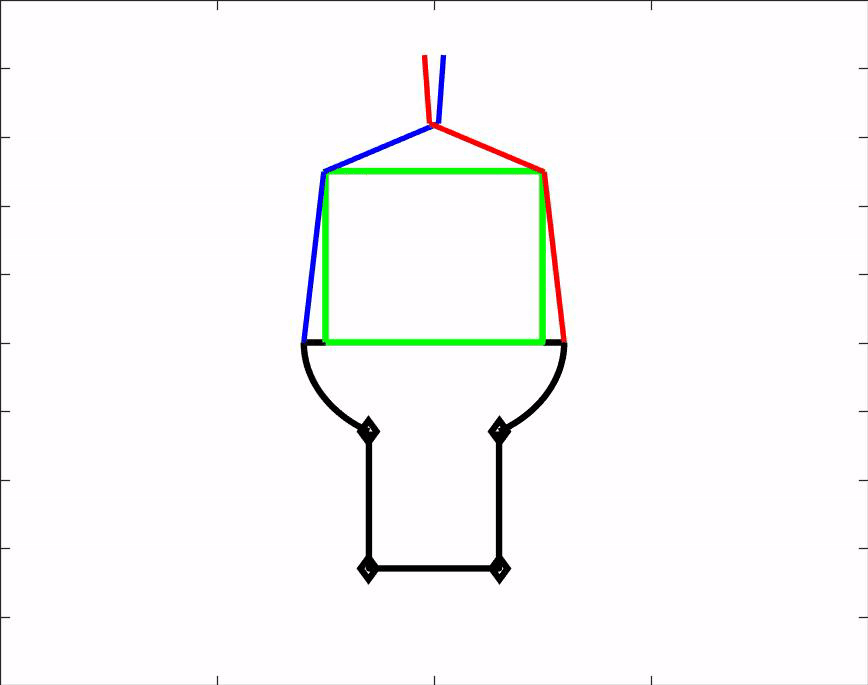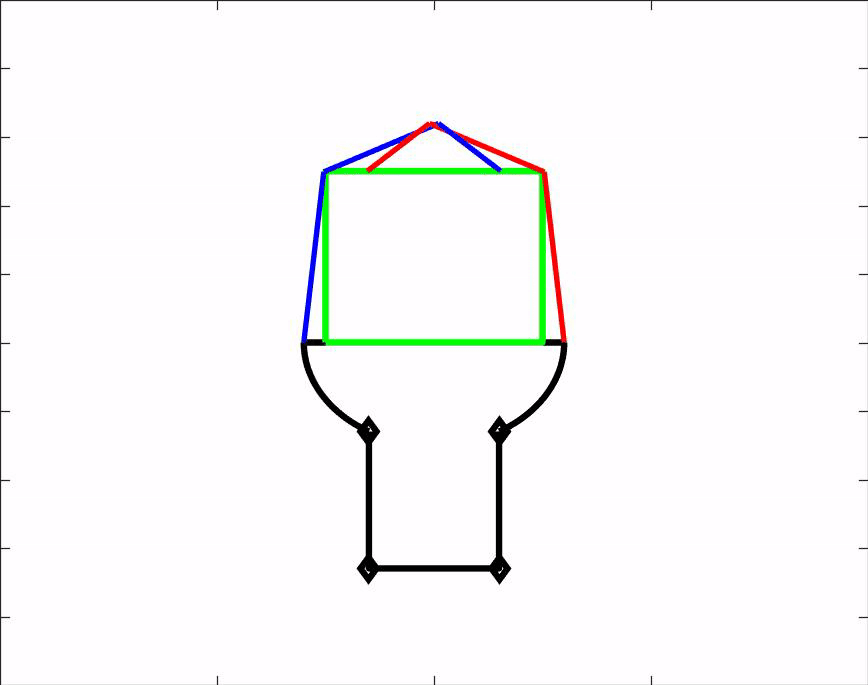
Om ons ontwerp te kunnen testen hebben wij een matlab script gemaakt. Dit script is een simulatie van onze hand en laat zien hoe de hand voorwerpen van verschillende groottes en vormen vastpakt. Het script kan dus gebruikt worden om vooraf te bepalen of een voorwerp gepakt kan worden door onze grijper. Daarnaast geeft het ons nuttige informatie over de hoeken waaronder de vingers uiteindelijk komen te staan. Download het MatLab script