Ontwerp
Grijper
Iedereen heeft een eigen idee voor grijper getekend. Hieronder staan alle ideeën op een rij:
Lizan
Tessa
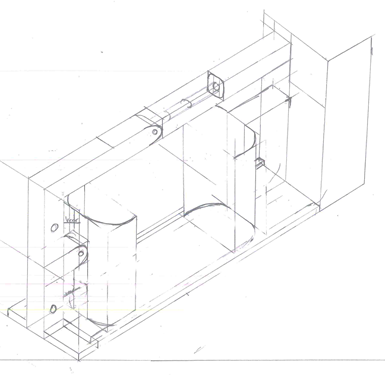
Jasper
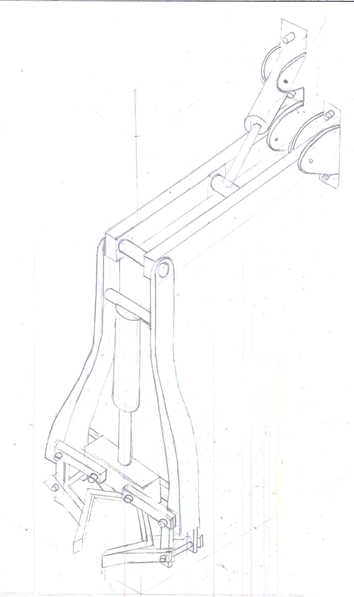
Robbie
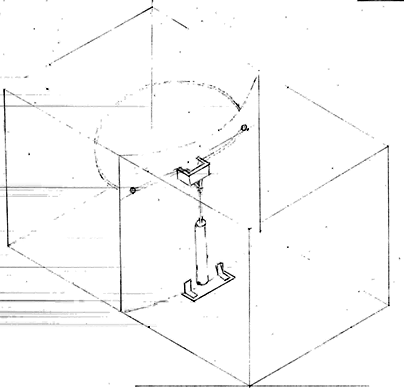
Frank
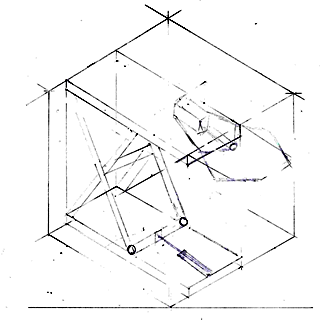
Daan
Na allen een eigen ontwerp gemaakt te hebben was het tijd om het beste ontwerp te kiezen. Dit hebben wij gedaan aan de hand van onderstaande tabel. Hierin hebben we alle aspecten van de grijper die voor ons belangrijk zijn verticaal geplaatst en alle ontwerpen horizontaal. Ook hebben we een factor toegevoegd, hiermee kunnen wij heel makkelijk bepaalde aspecten belangrijker maken dan andere. Na het opstellen van de tabel zijn we voor elk ontwerp cijfers tussen de 1 en 5 gaan geven per aspect. Na alle ontwerpen beoordeeld te hebben kwam het ontwerp van Jasper als winnaar uit de bus. Dit zijn we daarna ook verder uit gaan werken.
| Factor | Lizan | Tessa | Jasper | Robbie | Frank | Daan | |
|---|---|---|---|---|---|---|---|
| Stabiliteit | 5 | 2 | 3 | 4 | 3 | 2 | 3 |
| Snelheid | 2 | 3 | 4 | 1 | 3 | 4 | 4 |
| Duurzaamheid | 2 | 3 | 4 | 2 | 2 | 5 | 4 |
| Eenvoud | 4 | 4 | 2 | 2 | 2 | 4 | 4 |
| Grip | 4 | 2 | 2 | 5 | 3 | 1 | 3 |
| Draagkracht | 3 | 2 | 3 | 5 | 4 | 2 | 3 |
| Afstelbaarheid | 5 | 1 | 1 | 4 | 3 | 2 | 3 |
| Esthetiek | 1 | 5 | 2 | 3 | 4 | 3 | 3 |
| Totaal | 130 | 62 | 63 | 92 | 76 | 67 | 86 |
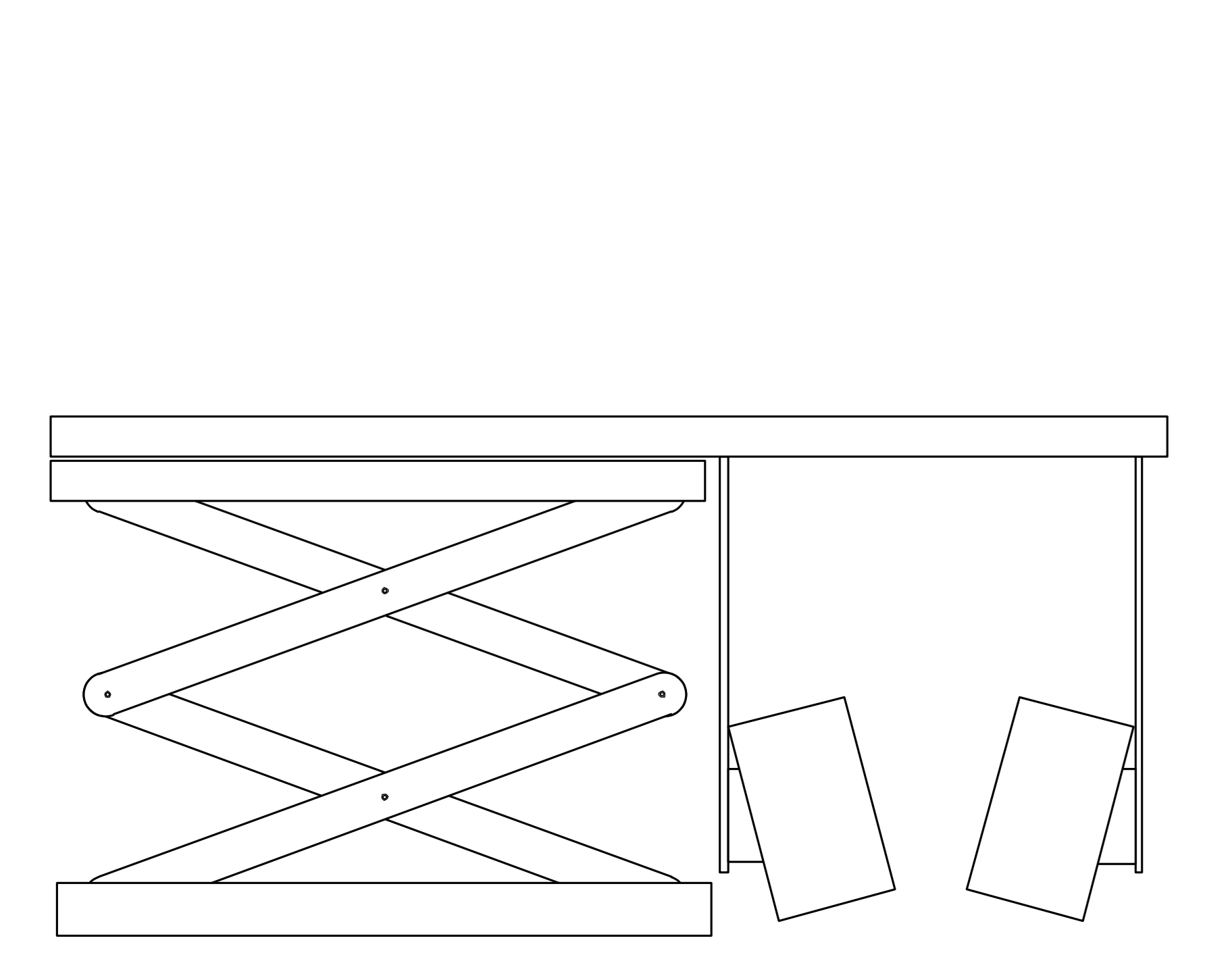
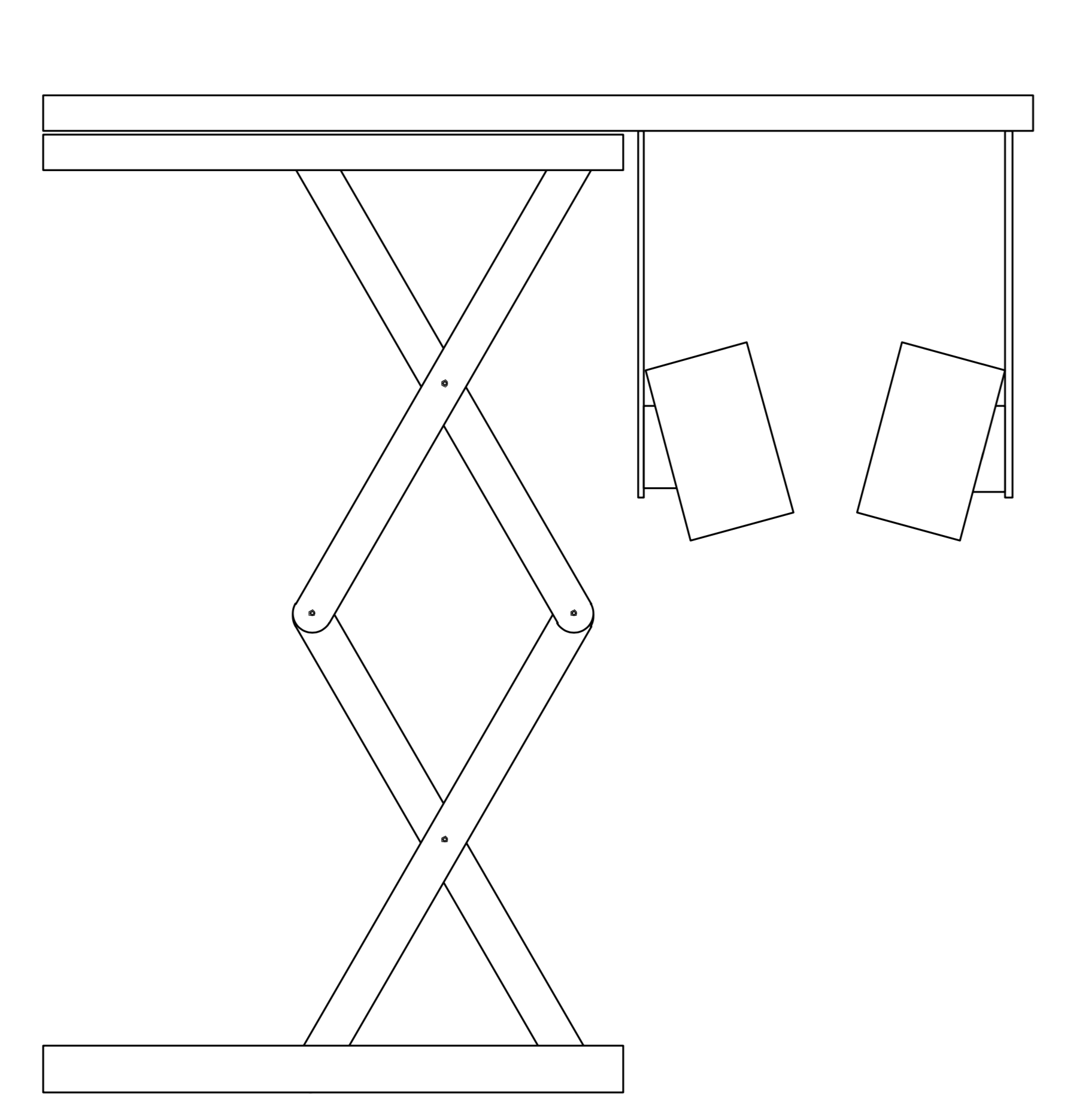
Lift
Na het kiezen van de grijper moest er nog gekozen worden voor een manier om de beker omhoog te krijgen. Hiervoor kwamen wij al snel uit op een schaarlift, dit kwam door de volgende punten:
- Stabiel, door het gebruik van 2 armen en 4 aangrijpingspunten blijft het platform stabiel.
- Het platform blijft vlak, het vlak blijven van het platform is essentieel voor het grijperontwerp dat we hebben.
- Eenvoud, door het gebruik van weinig moeilijke vormen en een gemakkelijke fabricage is dit ontwerp erg haalbaar voor ons team.
Na het kiezen van de schaarlift moesten we er berekingen aan doen. Dit om te kijken hoeveel graden verschil er nodig was voor de gewenste hoogte, en of het haalbaar was met de actuator die we hadden. Om deze beide berekeningen te vereenvoudigen hebben we het berekend met MATLAB. Hieronder zijn de 3 grafieken uit het MATLAB bestand te zien, en kunt u hier het .m-file bekijken. U kunt klikken op de grafieken voor een vergroting.
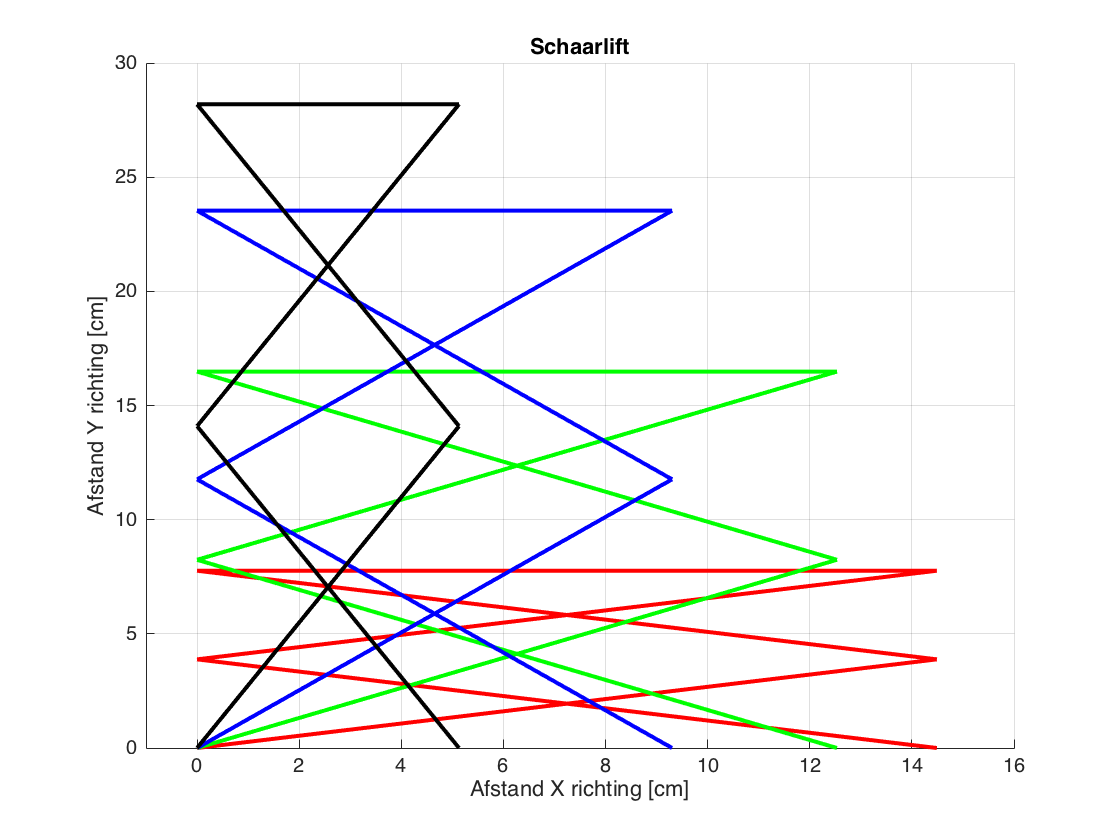
Grafiek 1
Op deze eerste grafiek is de volledige schaarlift in 2D te zien. Hierin zijn de armen afgebeeld voor de volgende standen: 15°, 33°, 55° en 70°. We hebben deze grafiek vooral gemaakt om een beeld te kunnen schetsen van de beweging die de schaarlift maakt.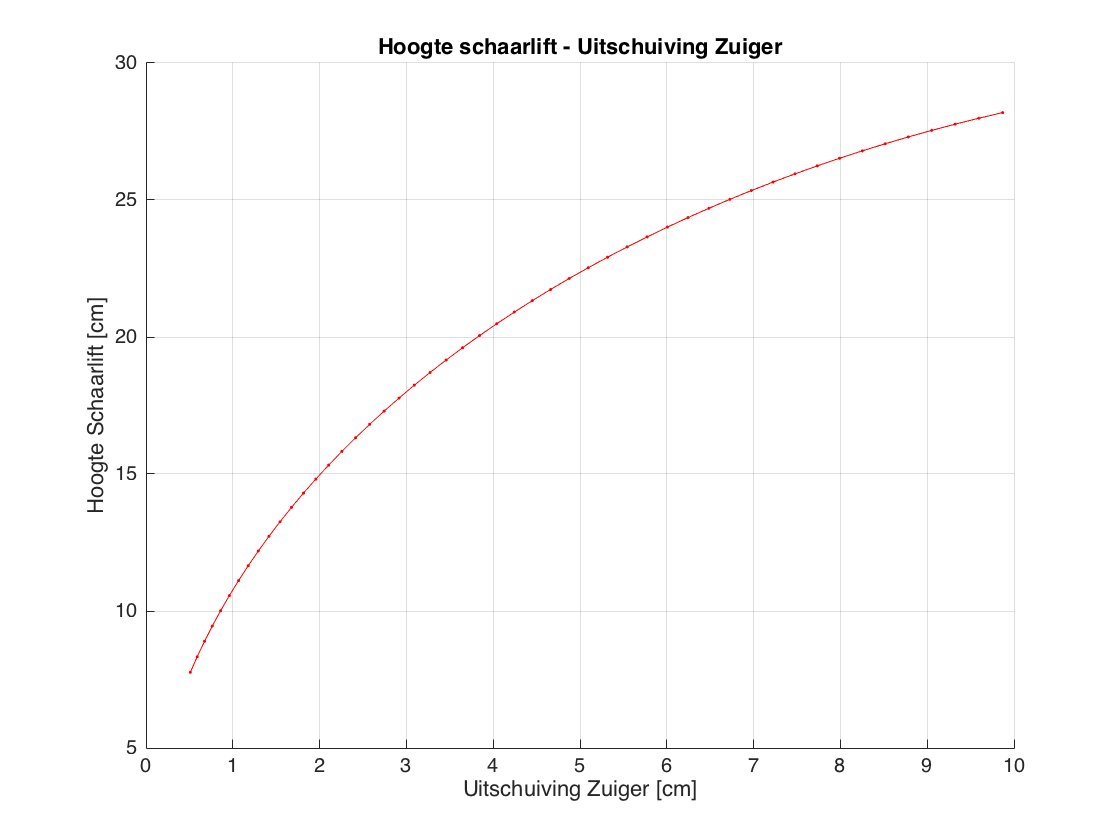
Grafiek 2
Op de 2e grafiek hebben we het verband tussen de actuator en de hoogte van de schaarlift onderzocht. Hieruitblijkt dat het een niet lineare beweging is, dit betekent dat de schaarlift niet een bepaalde afstand verplaatst voor het uitschuiven van de actuator.
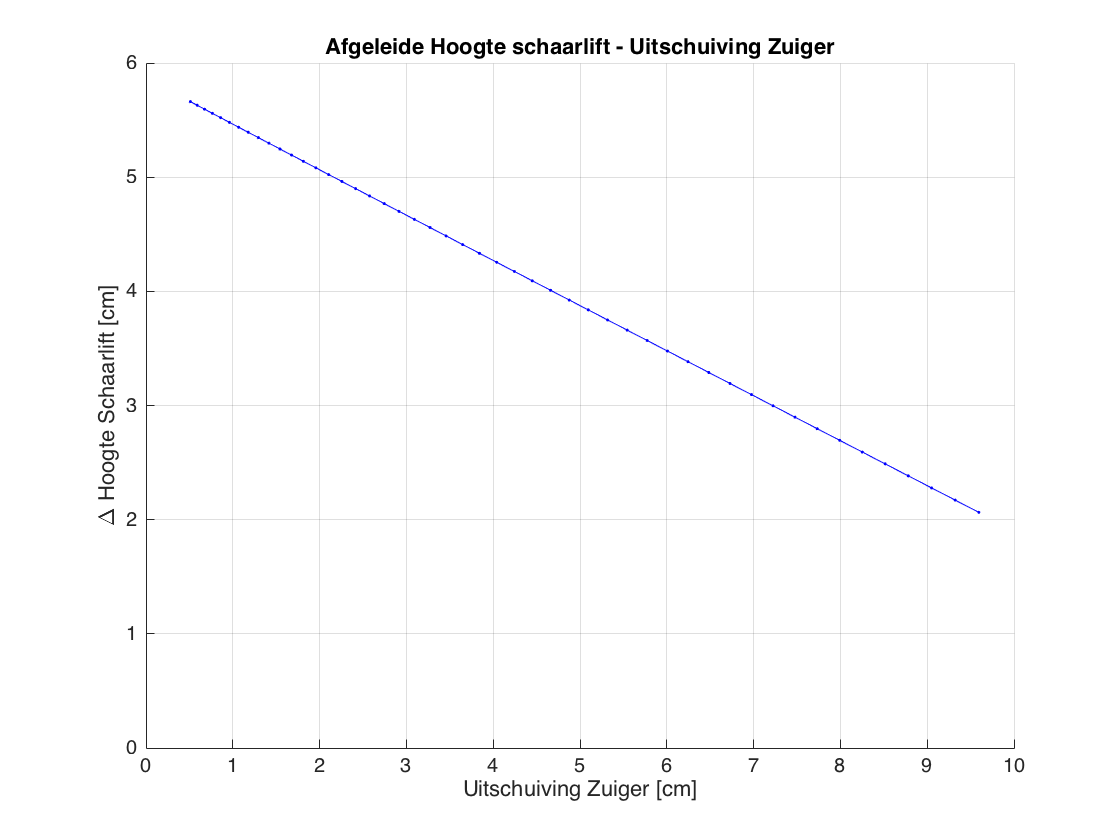
Grafiek 3
Op de 3e grafiek hebben we de afgeleide van grafiek 2 afgebeeld. Hierin is een lineare formule te zien, hieruit kunnen we afleiden dat hoogte van de schaarlift zich als een parabool gedraagt. Dit betekent dat in het begin van de beweging de hoogte sneller veranderd dan aan het einde van de beweging.
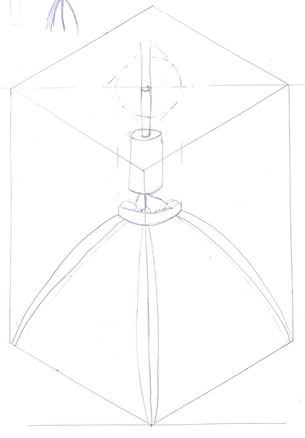
Eindontwerp
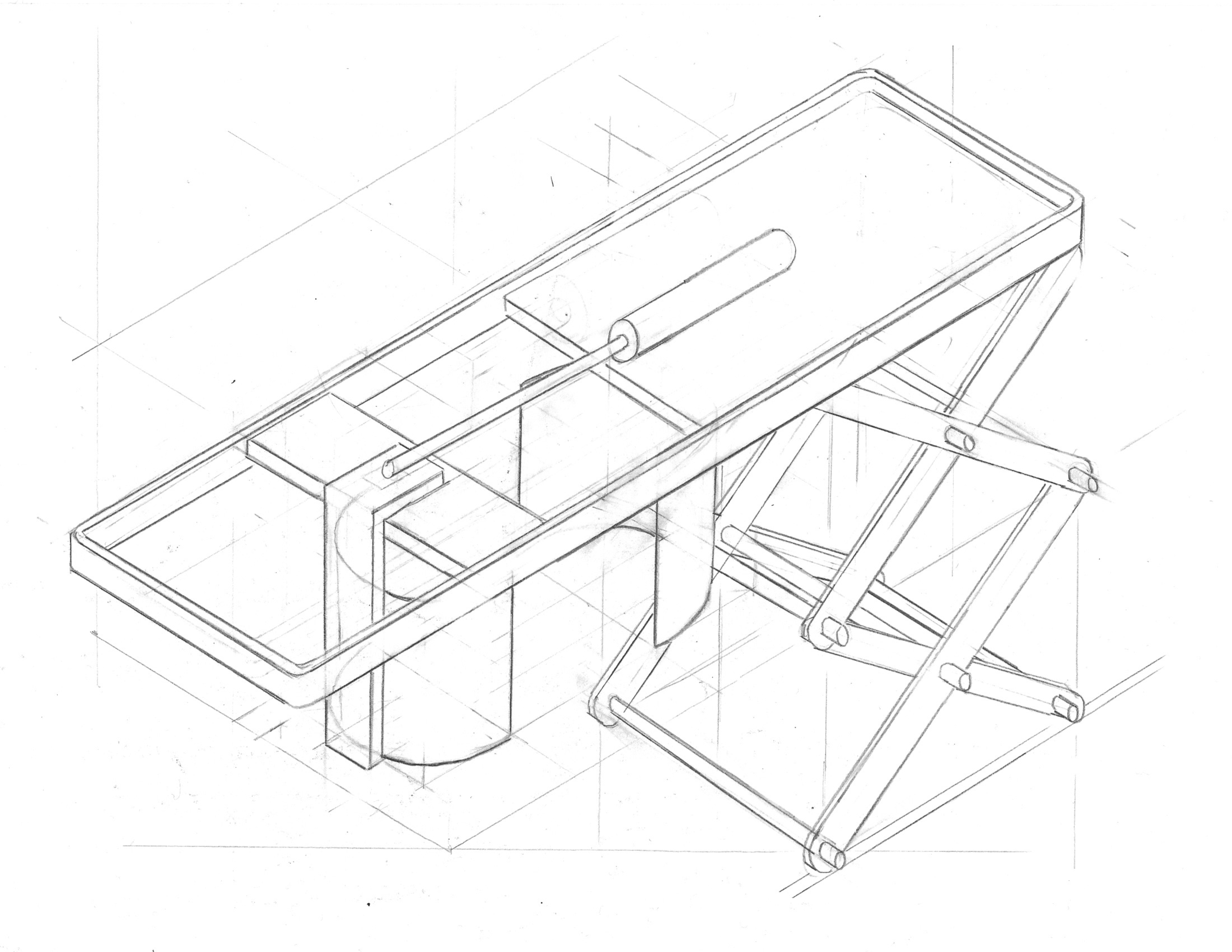
Schets
Door het samenvoegen van het idee van Jasper en de schaarlift, is bovenstaande ontwerp ontstaan. De schets is in isometrisch perspectief getekend.
MS Visio 1
Hierboven staat het ontwerp schematisch weergegeven in werkelijke verhouding. Het is weergegeven in ingeklapte en uitgeklapte stand van de schaarlift.
