eisen
Voor ontwerpopdracht 1 kregen wij allemaal de taak om een grijper te bedenken en te tekenen. We hoefden er nog niet op te letten of de grijpers zouden werken. Nadat wij hierover gezamenlijk gebrainstormd hadden, kwamen daar de volgende schetsen uit:
Om onze uiteindelijke grijper te kunnen kiezen uit de ontwerpen te kiezen, moesten we een lijst maken met eisen, waarin de eigenschappen stonden waar onze grijper aan moest voldoen . Ook moesten we de eisen rangschikken van belangrijk naar minder belangrijk en aan deze eisen een waarde toekennen.
Ons ontwerp moest aan de volgende eisen voldoen:
- Haalbaarheid, 10 punten: Is het ontwerp dat we kiezen wel mogelijk om te maken met de kracht van de actuatoren en de hoeveelheid materiaal die we tot onze beschikking hebben.
- Nauwkeurigheid, 8 punten: Kan onze grijper een bekertje oppakken zonder deze om te stoten en/of er veel uit te laten vallen.
- Stabiliteit, 7 punten: Is de grijper goed te monteren aan de wand die we mogen gebruiken.
- Veiligheid. 8 punten: Kunnen we met onze grijper veilig met de overgang van 1 naar 9 omgaan zonder dat het bekertje wordt gelanceerd of iets dergelijks.
- Demonteerbaarheid, 6 punten: Is onze grijper makkelijk aan de muur te monteren en kunnen de actuatoren er gemakkelijk in worden geplaatst.
- Snelheid, 3 punten: Kan onze grijper het bekertje binnen korte tijd vastpakken en optillen.
- Uiterlijk, 1 punt: Hoe ziet onze grijper eruit en hoe kunnen we zorgen dat dit wel om aan te zien is, bijvoorbeeld de randen schuren.
- Bekerbehandeling, 8 punten: Is onze grijper in staat om de bekertjes op te pakken zonder deze helemaal fijn te knijpen.
Nadat alle schetsen gemaakt waren door iedereen, hebben we deze allemaal met elkaar vergeleken en beoordeeld. Hiermee kwamen we tot de volgende scores:
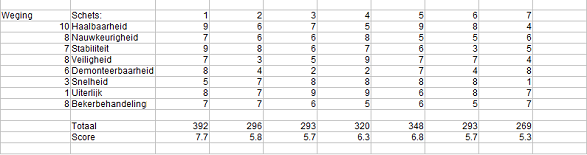

Schets 1, en tevens ons uiteindelijke ontwerp. We hebben voor deze schets gekozen omdat het aan al onze criteria voldeed. Wat deze grijper zo speciaal maakt is het feit dat er door de verschillende ringen in midden er verschillende maten bekers gepakt kunnen worden zonder de grip erop te verliezen.
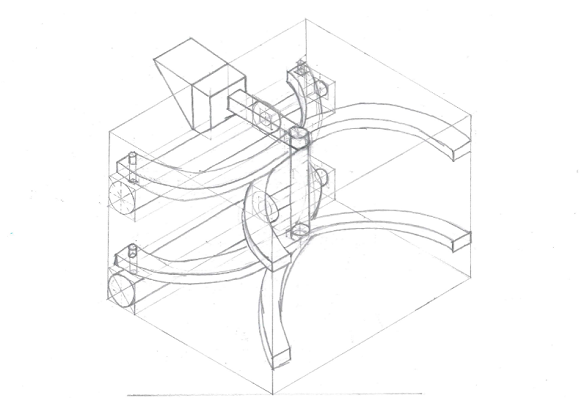
Schets 5, was onze 2e keus. Deze grijper was bijna het uiteindelijke ontwerp geworden. De reden dat deze schets zo hoog is geëindigd in onze lijst is vanwege de tangconstructie. Dit biedt vele voordelen. Net als in schets 1 kan deze de breedte van zijn grijper aanpassen en waardoor we veel grip zouden houden op de beker. Helaas leek ons de constructie een stuk onnauwkeuriger en minder stabiel dan de bovenstaande schets en daarom hebben we niet voor deze grijper gekozen.
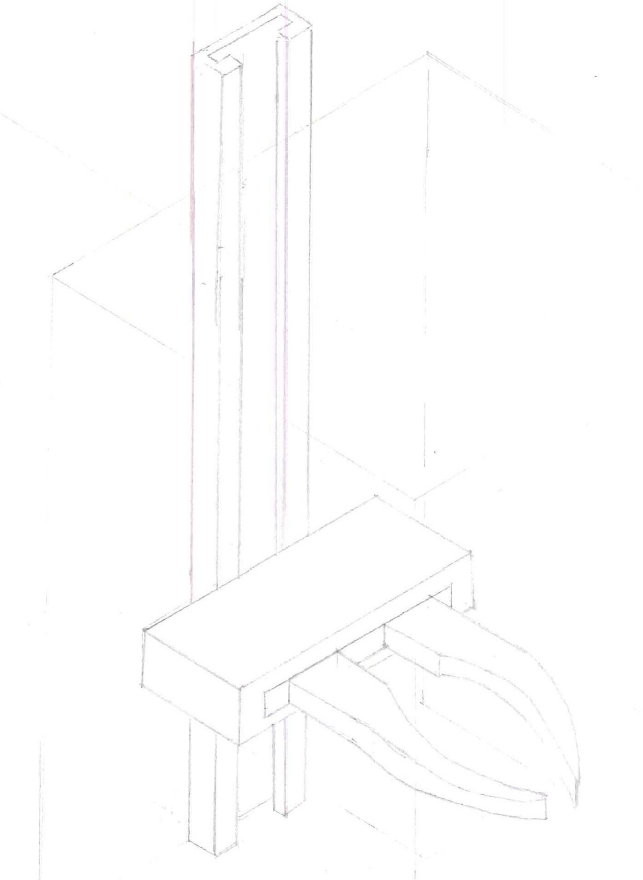
Schets 4 was onze 3e keus. Dit ontwerp is zo hoog geëindigd in onze lijst omdat het ons een zeer solide, veilig, nauwkeurig en snel ontwerp leek, maar net als voor schets 5, de bovenstaande, geldt dat er meerdere criteria zijn dat alleen deze, en daar legde het ontwerp het toch op af. Onze grootste twijfel was toch de demonteerbaarheid. Waar bij de bovenstaande 2 grijpers er nog een arm aan zit die makkelijk te monteren is aan de wand, leek dat ons een stuk lastiger met een soort van gleuf die vast gemaakt moet worden.
Analyse
Ontwerpopdracht 3 stond volledig in het teken van analyses. Gokken dat een ontwerp standhoudt is natuurlijk leuk en spannend, maar het maken van wat korte analyses kan een hoop onnodige moeite besparen. Met dit in ons achterhoofd en gewapend met whiteboardstiften, een rekenmachine en een lijst met afmetingen van de concept-grijper betraden we Meetingroom 1.3 in EWI. Een ding was zeker: deze dag zou een analytische slachting in de geschiedenis van WB9 markeren.
En zo geschiedde: We hebben die dag honderden nummers en formules opgeschreven en hebben daarmee belangrijke ontwerpkeuzes gemaakt. Er zijn acht analyses gemaakt: vier ervan grafisch, vier numeriek.
1. De gesloten klauw
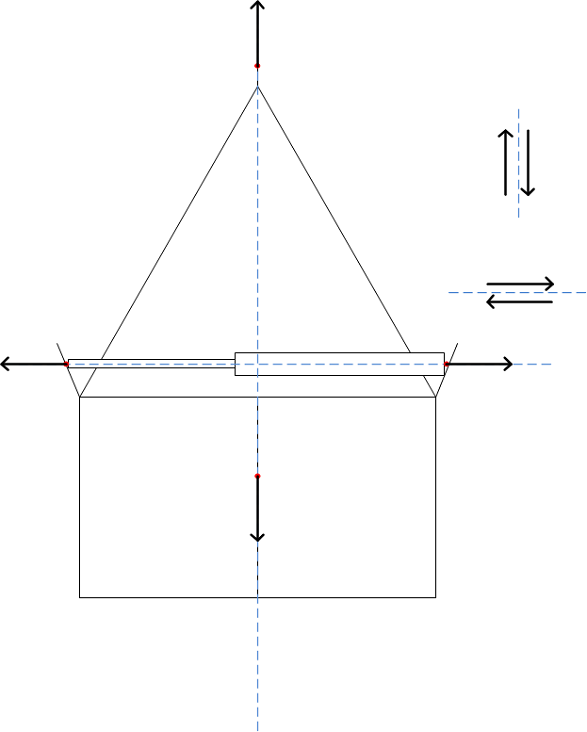
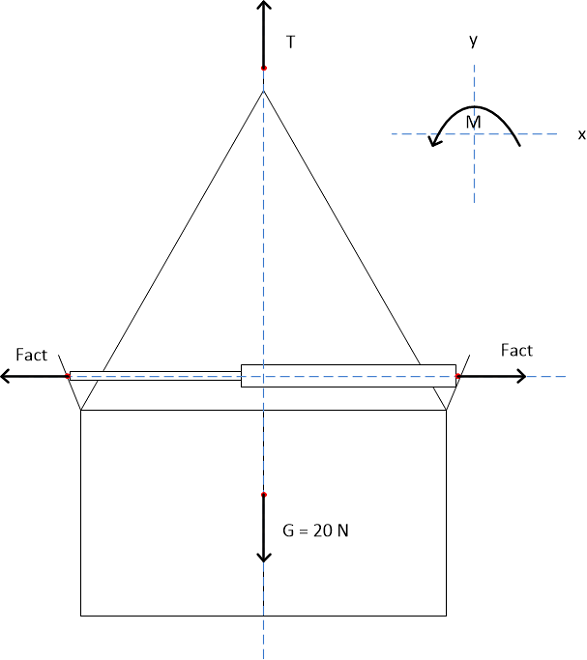
De analyse van de gesloten klauw is erg belangrijk: uit deze analyse moet namelijk blijken hoe groot de kracht op het ophangmechanisme van de grijper is. We kijken in deze analyse ook naar de grootste kracht die de actuator op het systeem uitoefent. De analyse zelf is gelukkig vrij simpel.
Er geldt dat ∑Fy=0, dus het gewicht G van de grijper en het bekertje samen moet worden gecompenseerd door de ophangkracht T. Het gewicht van de grijper is maximaal 15 N en het gewicht van het bekertje is maximaal 5 N. Met een totaal gewicht G = 20 N geldt dat T = 20 N. Deze kracht zou zonder plastische deformatie moeten kunnen worden verdragen door het ophangmechanisme.
Er geldt dat ∑Fx=0, dus de kracht die de actuator op beide kanten van de grijper uitoefent is even groot en tegengesteld. De grootte van deze kracht kan worden berekend met F=p*A, waarbij p de luchtdruk in de actuator is en A het oppervlak waar deze druk op werkt, in dit geval de uitschuivende staaf van de actuator. De luchtdruk is in de meest kritieke stand, als de grijper net niet open gaat, 9 bar = 9*105 Pa. De oppervlakte van de onderkant van de ronde pen is πr2= π*0.0032=0.00009π m2. Hieruit volgt dat de kracht van de actuator op de grijper 25.6 N is. Hoewel dit voor een grote kracht op beide kanten van de klauw zorgt en dus voor een vrije hoge versnelling en een grote openslaande ‘klap’, moet de klauw deze kracht in theorie kunnen verdragen. Het is wel aan te raden om een kleine aanpassing in de constructie te maken, bijvoorbeeld door het gebruiken van een sterke trekveer, om de klap enigszins op de vangen en zo de vervorming en vermoeiing van het materiaal tegen te gaan.
2. De open klauw
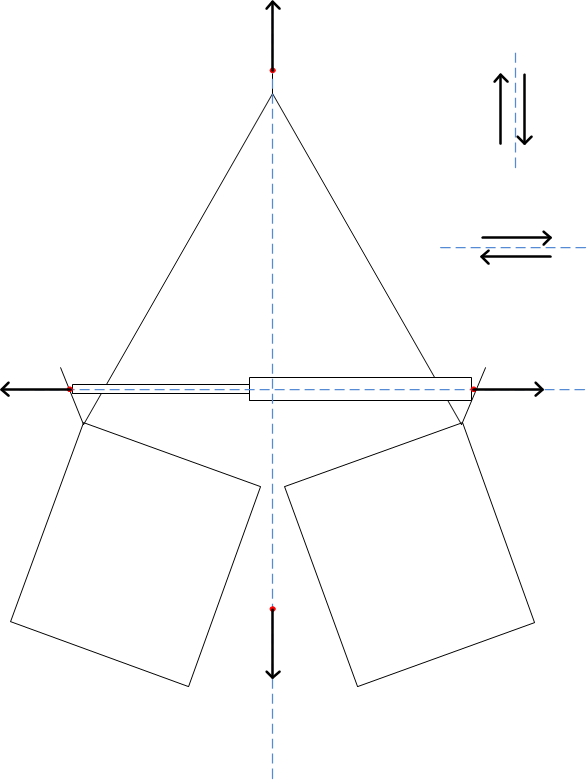
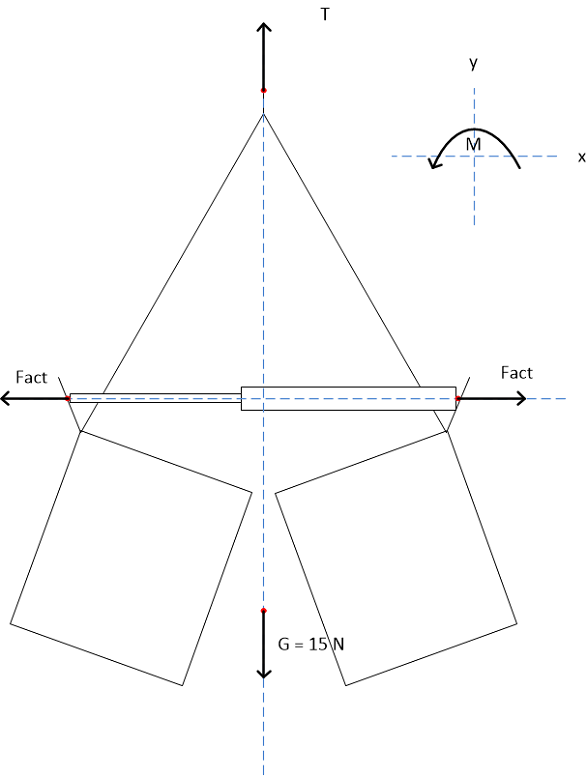
Uit de analyse van de open klauw moet blijken of er geen grote veranderingen plaatsvinden ten opzichte van de situatie met de gesloten klauw. Omdat de klauw symmetrisch is, hebben we namelijk het vermoeden gekregen dat er in deze situatie maar weinig verandert ten opzichte van de situatie met de gesloten klauw. De analyse verloopt, net als de analyse van de gesloten klauw, vrij simpel.
Er geldt ∑Fy, dus het gewicht G van de grijper moet worden gecompenseerd door de ophangkracht T. Met G = 15 N geldt dat T = 15 N. Deze kracht zou zonder plastische deformatie moeten kunnen worden verdragen door de klauwconstructie.
Er geldt dat ∑Fx=0, dus de kracht die de actuator op beide kanten van de grijper uitoefent is even groot en tegengesteld. De grootte van deze kracht kan berekend worden met F=p*A, waarbij p de luchtdruk in de actuator is en A het oppervlak waar deze druk op werkt, in dit geval de uitschuivende staaf van de actuator. De luchtdruk is in de meest kritieke stand, als de grijper net niet open gaat, 9 bar = 9*105 Pa. De oppervlakte van de onderkant van de ronde pen is πr2= π*0.0032= 0.00009π m2. Hieruit volgt dat de kracht van de actuator op de grijper 25.6 N is. Deze kritieke stand vindt plaats bij rust: er is geen sprake van een klap tegen het materiaal aan. Dit zorgt ervoor dat deze kracht vrij makkelijk door de constructie wordt opgevangen.
3. De grijper in de hoogste stand
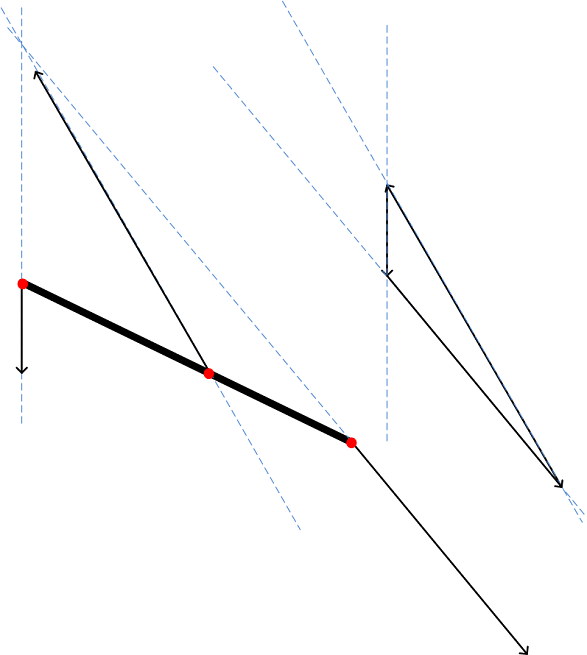
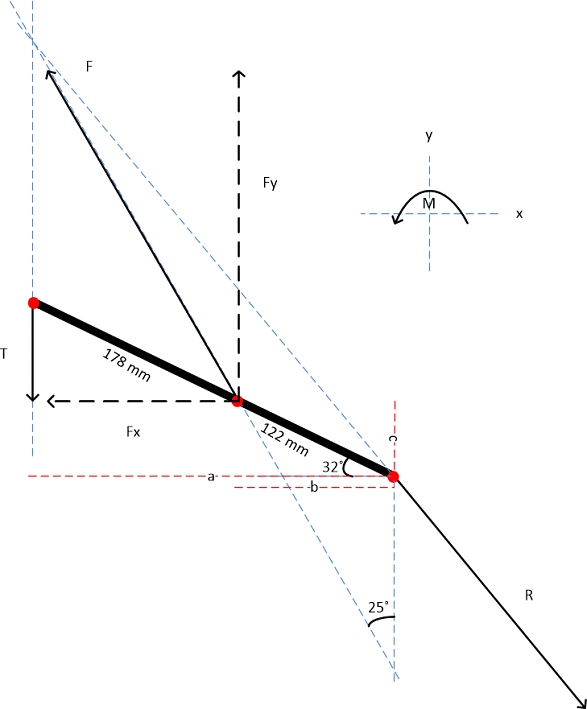
Uit deze krachtenanalyse moet worden bepaald hoe groot de veercompensatie moet zijn om de grijper niet met een harde klap in de bovenste stand tot rust te moeten komen. De numerieke krachtenanalyse bevat veel goniometrie. Voor een duidelijker overzicht staan hieronder de benodigde constanten met de goniometrie erin doorgerekend.
a = 300cos(32°) mm
b = 122cos(32°) mm
c = 122sin(32°) mm
T = 20 N
Er moet gelden dat er in de bovenste stand een statisch evenwicht is. De kracht van de actuator is bekend:
Fact = p*A = 9*105*0.003π = 27π ≈ 84.8 N
Daarnaast kan aan de hand van goniometrie gezegd worden dat Fx= tan(25°)Fy. Samen met de momentvergelijking ∑Mo=a*T+c*Fx-b*Fy=0 levert dit een stelsel vergelijkingen op, waaruit Fx en Fy kunnen worden berekend:
a*T + c*Fytan(25°)- b*Fy = 0
Fy*(-c*tan(25°)+b) = a*T
Fy = a*T/(-c*tan(25°)+b)= 59.9 N
Fx= tan(25°)*59.9 = 27.9 N
Met deze Fx en Fy kan F, de maximale kracht uit de richting van de actuator op het systeem, aan de hand van de stelling van Pythagoras worden berekend:
F = √((27.9)2+(59.1)2)=66.1 N
De veercompensatie Fveer van de trekveer volgt hieruit door het absolute verschil tussen Fact en F te nemen:
Fveer = |66.1-84.8| = 18.7 N
De uitrekking van de veer is gelijk aan de uitrekking van de actuator: u = 0.1 m. Hieruit volgt de veerstijfheid: k = 18.7/0.1=187 N/m. Uit deze berekening volgt daarnaast dat k moet stijgen bij een daling van T: de berekende veerstijfheid is dus de minimaal benodigde stijfheid.
4. De grijper, net vertrokken uit de laagste stand
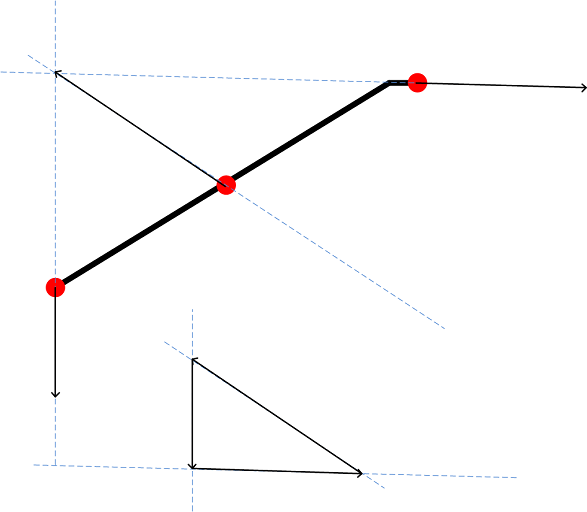
.png)
Uit deze krachtenanalyse moet worden bepaald of de eerder berekende veercompensatie niet te groot is, waardoor de actuator niet zou kunnen uitschuiven. Omdat de numerieke analyse veel goniometrie bevat, zijn hieronder een aantal belangrijke constanten weergegeven:
e = 10 + 300cos(28°)
f = 10 + 122cos(28°)
g = 122sin(28°)
Fx = tan(44°)*Fy
Er geldt ∑Mo=e*T-g*Fx-f*Fy=0. Er kan nu een stelsel vergelijkingen worden opgesteld, waaruit de waardes van Fx en Fy kunnen worden berekend:
e*T - g*Fx – f*Fy= 0
e*T = g*Fx + f*Fy
e*T = g*Fytan(44°) + f*Fy
Fy(g*tan(44°)+f) = e*T
Fy = e*T/(g*tan(44°)+f)=23.4N
Fx = tan(44°)*23.4 = 22.6N
Met deze Fx en Fy kan F, de maximale kracht uit de richting van de actuator op het systeem, aan de hand van de stelling van Pythagoras worden berekend:
F = √((22.6)2+(23.4)2)=32.5 N
De benodigde actuatorkracht is de optelling van F en Fveer: Fact = 1.87 + 32.5 = 34.4 N. De actuator kan een maximale kracht Fact leveren van Fact = p*A = 9*105*0.003π = 27π ≈ 84.8 N. De actuator is dus sterk genoeg om de constructie op te tillen.
bouwen
De vierde ontwerpopdracht stond in het teken van het fabriceren van de grijper. We moesten ons ontwerp, nu echt gaan bouwen. Je kon zelf materialen bij elkaar zoeken, maar er was ook de mogelijkheid om gebruik te maken van een perspex plaat van 490 X 240 X 5 mm, die voor ons werd laser gesneden. Om gebruik te kunnen maken van de uitgesneden perspex onderdelen moesten we de onderdelen op een template tekenen. Dit was de werktekening voor de lasersnijder, hiervoor golden een paar voorwaarden:
- De afstand tussen de onderdelen moest minimaal 2.5 mm zijn.
- De totale omtrek van de onderdelen moest maximaal 9000 mm zijn.
De tweede voorwaarde was een klein probleem voor ons, want in eerste instantie was de omtrek meer dan 10 meter. Om toch onder de 9 meter te komen hebben we de armen tegen elkaar geplaatst. We zouden deze armen later doorzagen.
Het duurde een week voordat de onderdelen weer terug waren en in die tijd hadden we de bouten, moeren en veren bij elkaar gezocht, zodat we de grijper snel in elkaar konden zetten.
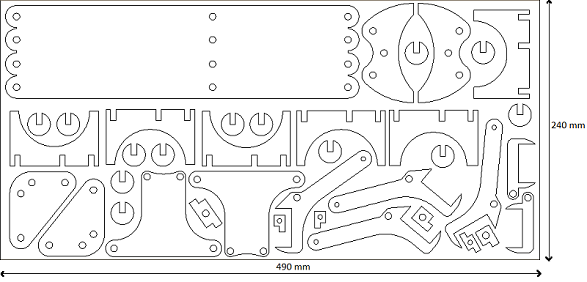
We hadden de lasersnijder ook de gaten laten snijden, zodat we ook geen gaten meer hoefden te boren. Het enige probleem was het los zagen van de armen, want met een figuurzaag lukte dit niet. Het lukte wel door over de gehele lengte van de armen gaten te boren met een kolomboor en de armen vervolgens eraf te breken. Dit ging bij drie van de vier armen goed, maar bij de vierde arm ging dit verkeerd moet dit met superlijm worden hersteld. Waarna we de grijper in elkaar konden zetten. Er was alleen een ontwerpfout in ons idee, want de grijper raakte de arm vanaf een bepaalde hoogte, maar dit had verder geen invloed op de te behalen hoogte van 25 centimeter.

Test
Inmiddels hadden we onze grijper gebouwd. Hierna gingen we de grijper testen om erachter komen of de grijper aan onze verwachtingen voldeed. Om dit te meten stelden we een testplan op van wat we precies aan de grijper wilden testen.
Testplan:
1. De snelheid waarmee het bekertje tot 25 cm wordt opgetild.
2. De maximale tilhoogte.
3. Of de beker en de inhoud intact blijven tijdens het proces.
4. De minimale en maximale beker omtrek die de grijper kan tillen.
5. Het gewicht van de grijper.
6. De massa die de grijper kan tillen.
1. De snelheid waarmee het bekertje tot 25 cm wordt opgetild: s=0.25 m

De gemiddelde snelheid van de grijper is dus 0.30 m/s met een meetnauwkeurigheid van 0.015 s ≡ 0.0038 m/s.
2. De maximale tilhoogte

De maximale tilhoogte is 0.265 m met daarbij een meetonnauwkeurigheid van 0.00408m. Dit is hoger dan de benodigde hoogte waar wij vanuit waren gegaan van 0.25 cm.
3. De grijper hebben we bekers van verschillende soorten materiaal laten optillen, respectievelijk dik karton, dun karton en plastic. Alle bekertjes bleven hierbij intact bij het sluiten van de grijper.
Ook hebben wij een beker gevuld met verschillende soorten materialen, namelijk water, papiersnippers en bouten. Dit alles bleef in de beker zitten terwijl de grijper sloot en de beker werd opgetild.
4. De minimale en maximale beter omtrek die de grijper kan optillen

De minimale omtrek die een beker kan hebben is 188.5 mm en de maximale omtrek is 205.9 mm met een meetonnauwkeurig van 0.151 mm. Dit wijkt vrijwel niet af van de theorische waarden van 188.5 mm en 207.3 mm.
5. De massa van de grijper is respectievelijk 655 gram gemeten met een weegschaal met een meetonnauwkeurigheid van 5 gram.
6. De massa die de grijper kan dragen is de vereiste 500 gram en daarbij ook nog zijn eigen massa. Deze massa is dus 1155 gram. Dit ligt onder de massa die wij hadden bepaald dat de grijper maximaal zou kunnen dragen.













.png)





